Standard Convex Model Flaw? Hurricanes and Weather: Rethinking Storm Formation Inside a “Concave Earth”

TRUEMODELOFTHEWORLD · December 23, 2024, 9:54pm

Hurricanes in a Bowl? Rethinking Storm Formation Inside a “Concave Earth”

Introduction

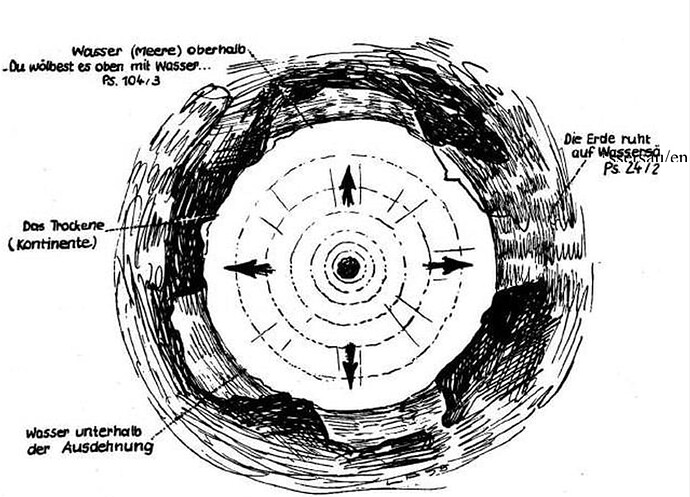
When most people imagine Earth, they picture a round sphere on which we live on the outside. Our globe spins, generating a slight bulge at the equator, and we rely on classical gravity—originating from Earth’s mass—to hold us firmly on the ground. But what if that picture were inverted? Some alternative theories propose a concave Earth: we live on the inside of a vast spherical shell, with “gravity” pushing outward against that shell.

At first glance, this might seem purely speculative. However, hurricane dynamics—particularly their spiral structure and funnel‐like “eye”—offer a compelling testbed for exploring whether concavity might actually make storms more intuitive. This article takes a critical, devil’s‐advocate approach to see how a Concave Earth could, in principle, explain large‐scale storms more naturally than the standard model.

1. The Power of a Bowl: A “Toilet‐Flush” Analogy

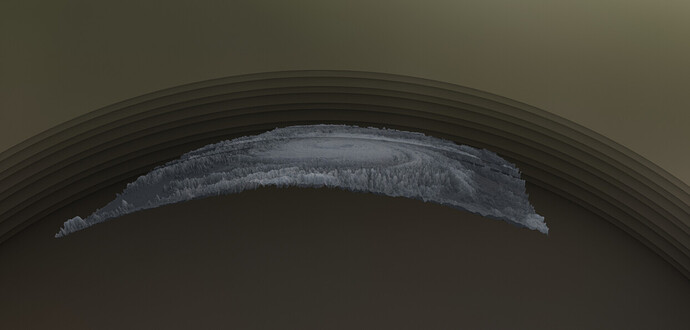
Have you ever watched water swirl down a toilet or a sink? The concave shape of the bowl helps direct fluid toward a single drain. If the surface were convex, water would slide off in all directions—less likely to form a tight funnel.

Hurricanes, on our standard globe, arise from warm, moist air rising and converging into a low‐pressure center. As the planet’s rotation (or the rotating atmosphere) deflects air currents—via the Coriolis effect—the system begins to spin, eventually creating the swirling wind bands we recognize from satellite images. In the concave Earth viewpoint, however, the ground itself forms a giant inward “bowl,” potentially creating a more direct geometric funnel effect as air swirls around and pools at the “lowest point.”

Does the “bowl shape” amplify funnels?

Standard Model: The funnel shape arises primarily from local fluid dynamics, temperature contrasts, and rotation.
Concave Model: Envisions an actual “bowl,” so swirling air might naturally converge and intensify more rapidly, much like water draining down a sink.

2. The Scale of Curvature: More Significant Than You Think

Critics often point out that Earth is huge, making the curvature over a few hundred kilometers (the diameter of a hurricane) relatively small. Indeed, on a globe of radius ~6,371 km, you only get about 5 km of rise or fall across a 500 km “chord.” In typical meteorology, 5 km may seem marginal compared to the 10–15 km thickness of the troposphere.

Yet from the devil’s‐advocate perspective, 5 km is half the lower atmosphere’s depth. If you superimpose that difference onto a hurricane, the subtle background bowl vs. dome could alter vertical pressure surfaces, slightly reorient airflow, and potentially focus the funnel.

Convex Earth: That 5 km difference curves downward (like a dome), potentially reducing the impetus for air to swirl into a single eye.
Concave Earth: The same 5 km difference curves upward (a basin), perhaps giving air a more direct path to converge into a “center well.”

Though mainstream meteorologists typically find these differences negligible, a concave proponent might suggest the geometry is enough to enhance swirling convergence—particularly for storms spanning hundreds of kilometers.

3. Gravity: Is It Really from Mass, or Could It Be “Outward” Pressure?

In conventional physics, gravity comes from Earth’s mass, pulling objects down toward its center. In the concave Earth idea, “gravity” might instead be a push from a cosmic‐scale or etheric pressure—effectively forcing everything outward onto the inside surface of a sphere.

Why Does This Matter for Hurricanes?

Standard (Convex) Earth: The atmosphere is held against Earth’s outer surface by mass‐based gravity. Rotational forces (centrifugal, Coriolis) are relatively small but crucial for storm spin.
Concave Earth: Outward gravity combined with a daily rotation of the ether could still produce Coriolis‐like deflections. But the overall framework might more naturally direct airflow toward a central “eye” if that eye is the lowest point in a “bowl.”

This perspective can be reminiscent of water swirling in a drain—where the “down” is always to the drain in the center. On a convex planet, the “lowest point” is conceptually near the center of Earth, not on some localized patch of surface. So how do hurricanes still manage to tighten around an “eye”? The standard model says that’s just a function of pressure gradients and rotation. A concave model suggests it might be inherently geometric.

4. Could Concavity Actually “Win”? A Hypothetical Path to Falsifying the Globe

Most scientists see no contradictions in the rotating‐globe model: it explains everything from orbital mechanics to GPS signals with impressive consistency. Yet a real falsification would occur if we found data that standard spherical Earth meteorology can’t reconcile, while the concave model handles it effortlessly. Some possible lines of inquiry:

Precise Storm Shape Measurements
If high‐resolution data revealed that the vertical structure of hurricanes consistently forms a deeper “bowl” profile (or “dip”) than predicted by standard geostrophic flow models, that might suggest we live in an inward curvature.
Unexplained Funnel Intensification
If we discovered hurricanes strengthen far more quickly than the best spherical Earth fluid‐dynamic simulations predict—without large changes in sea‐surface temperature or wind shear—perhaps a missing “bowl effect” helps direct inflow more efficiently in a concave scenario.
Repeated Anomalies in Pressure Surfaces
If real measured isobaric surfaces (lines of equal atmospheric pressure) systematically deviate from the slight curvature expected on a standard globe, that discrepancy might be the smoking gun for a world that’s curved the other way.

In other words, if big storms regularly misbehave in a way that is suspiciously “bowl‐friendly,” it could poke a hole in our typical assumptions about living on the outside of Earth.

5. A Devil’s‐Advocate Conclusion

While mainstream science rests comfortably on the convex‐Earth model, a concave‐Earth concept does open the door to an intriguing possibility: that swirling, funnel‐like storms might form more naturally if Earth’s surface were shaped like the inside of a giant bowl. The curvature difference across a hurricane’s footprint—on the order of a few kilometers in vertical offset—may be large enough to influence atmospheric stratification, pressure gradients, and vortex intensification.

So could hurricanes really be the key to proving we live in a concave Earth?
That remains an extreme position, given the wealth of mainstream observations (satellite orbits, geodetic measurements, etc.) that align neatly with a convex globe. Nonetheless, in a thought experiment or if unforeseen data came to light, a concave geometry might explain certain funnel characteristics with fewer tweaks. In an alternate reality, or with future high‐resolution storm data, it’s conceivable that the concave Earth theory could find its “toilet‐bowl” moment—showing that giant swirling storms behave just a bit more like water spinning in an inverted basin than outward logic would suggest.

For now, standard meteorology seamlessly explains hurricanes without needing an inside‐out Earth. But every once in a while, it’s worth playing devil’s advocate to see if the shape of our planet might—quite literally—be turned inside out.

References & Further Reading

Holton, J. R. & Hakim, G. J. (2012). An Introduction to Dynamic Meteorology. Academic Press.
Emanuel, K. (2005). Divine Wind: The History and Science of Hurricanes. Oxford University Press.
Concave Earth Proposals (Various). Online resources describing “longitudinal ether pressure” and “outward gravity.”

Below is a secondary version of the article. Check it out if you enjoyed reading the above

Summary

Thought about concave vs. convex forces in hurricanes for 16 seconds

Below is an attempt at devil’s advocacy—doing our best to poke at potential “holes” in the standard heliocentric/convex model, while highlighting how a concave‐Earth geometry might (at least on the surface) offer a more intuitive or “toilet‐bowl–like” explanation of storm funnels. This does not mean mainstream science accepts these arguments; rather, we are temporarily flipping the script to see if the convex model can be undermined in favor of concavity, particularly regarding hurricane formation.

1. The “Bowl Effect” and Funnel Formation

1.1. Standard Model “Flaw”: Where Does the Funnel Energy Concentrate?

Convex Earth Explanation: Hurricanes arise primarily from warm moist air rising and being spun by Coriolis forces. The “funnel” or spiral structure is almost entirely a local fluid dynamic phenomenon.
Potential Hole: In a toilet bowl analogy, concavity helps water converge into a central drain. By analogy, might a concave Earth provide a natural “focus” or “drain” for swirling air currents, reinforcing the vortex at the center?
- On a convex surface, you’d expect the “lowest point” (in a purely geometric sense) to be along the chord between two points, rather than in some “center of a bowl.” So perhaps the flow shouldn’t so neatly converge into a single swirling funnel unless some external forcing is carefully fine‐tuned.
- Meanwhile, a concave geometry could “steer” air, at a fundamental level, toward one central point (the eye) more readily—like water swirling in the bottom of a bowl.

Devil’s‐Advocate View: If the Earth truly sloped downward away from the hurricane’s center in the convex sense, maybe we’d see the storm dissipate outward instead of forming a tight funnel at the middle. On a concave surface, the eye is physically the “lowest point” in the local region, helping to collect and concentrate swirling air in that one zone.

1.2. Does the Standard Model Overlook a “Focusing” Effect?

In normal meteorology, we say the funnel forms due to pressure gradients and rotation alone, ignoring any geometric “focusing.”
But if we imagine the concave Earth as literally shaped like an inward bowl, that curvature might focus rotating flows into a narrower column.
Could it be that the standard model is missing a subtle focusing phenomenon, requiring more contrived frictional or baroclinic adjustments to explain how “tight” the hurricane eye sometimes is?

2. The Measurable Curvature Within a Storm’s Diameter

2.1. Not So Negligible?

Mainstream Claim: Over ~500 km, Earth curves about 5 km, which is small but generally dwarfed by thermodynamic drivers.
Devil’s‐Advocate Twist: 5 km is half the thickness of the boundary‐layer portion of some storms. If the troposphere is ~10 km thick, a 5 km curvature difference is hardly trivial.
- On a convex Earth, you’d get a gentle “arch” downward across the diameter of the storm.
- On a concave Earth, that same arch is upward, creating more of a “basin” effect in the middle.
If real hurricanes do exhibit that “deep basin” shape in the vertical cross‐section, might it align better with concavity?

2.2. Could Observed Storm Data Subtly Favor an Inward “Bowl”?

Suppose you gather high‐resolution measurements of the vertical distribution of pressure surfaces across a massive hurricane. Maybe you discover they warp in more than standard geostrophic models predict.
You might interpret this “extra” dip or bowl as evidence that the surface below is also shaped inward, reinforcing that geometry.

Devil’s‐Advocate Angle: If we were on a concave Earth, the background shape of the troposphere would be a bowl, so the normal “isobaric surfaces” might deviate from the classical rotating‐sphere formulas in a systematic way. If we found consistent anomalies in real data that fit a “bowl model” better, that would be a hole in the standard spherical approach.

3. Gravitational/Pressure Gradients “Flipped”

3.1. If Gravity Is Actually a Pressure Pushing You Outward

Mainstream: Mass in Earth’s interior pulls you downward.
Concave: A “longitudinal pressure” from the ether pushes you outward to the shell.
The net effect is the same in everyday life (you feel weight), but if gravity is outward, the geometry of fluid statics might be re‐interpreted.

Devil’s‐Advocate:

In a concave model, perhaps vertical/hydrostatic equilibrium in storms lines up more naturally with swirling “inward” funnels, since the boundary itself is “the inside of a sphere.”
The standard model might have to do mental gymnastics: it says everything is pulled “down” to the center of Earth, yet we observe swirling that might seemingly want to “drain.” Could we be forcing the swirl to “drain” to Earth’s center (which is actually below us in the convex sense) instead of letting it “drain” in a more physically intuitive direction if we’re really inside?

3.2. Hurricanes’ Eye as the “Most Outward” or “Most Inward” Spot?

On a convex Earth, the eye is a region of lowest surface pressure, but physically that region is still above Earth’s center.
In a concave Earth, you might argue the storm’s eye is truly the “deepest dip” in the local area (if you see the shell curving up all around). Then the swirling air more naturally collects in that “depression.”

If you do fancy 3D computational fluid dynamics under a concave geometry, maybe you’d see swirl intensification that matches better with certain real‐life storm intensities—if you tune the “outward” gravitational effect and rotating ether properly.

4. Other “Loose Ends” That Could Embolden Concavity

4.1. The “Toilet‐Bowl” Parallel

Water flushing in a bowl is strongly guided by the walls of the bowl. The swirl is forced into that funnel shape, quickly intensifying as water drops downward.
Hurricanes are large‐scale, but if the Earth were a giant bowl on the inside, maybe there is a macro version of that same phenomenon.
Standard meteorology chalks the funnel up to Coriolis + pressure alone, but maybe it’s ignoring how “inward‐curving ground” speeds up swirling flows.

4.2. Potential Over‐Reliance on Adjusted Equations

The mainstream uses baroclinic and barotropic models for storms, adjusting constants and coefficients (drag, friction, condensational heating, etc.) to get “correct” results.
Perhaps that indicates we’re “shoehorning” everything into a spherical geometry, while in truth, a concave geometry would require fewer forced adjustments for real‐world storms.

In other words, maybe the simpler explanation is that everything is shaped like a bowl inside, and the standard model’s complexities arise because it’s “backwards.”

5. Could These Arguments Falsify the Heliocentric Model?

From a purely devil’s‐advocate standpoint, you could say:

If extremely precise, large‐scale 3D measurements of hurricane structure revealed a consistent “bowl pattern” that standard spherical Earth meteorology either can’t replicate or must artificially tweak, that might be strong evidence for a concave shape.
If storms systematically show funnel intensifications or pressure gradients that simpler models under a concave geometry (with outward gravity) predict naturally, while the mainstream model needs improbable fine‐tuning, it would be a serious blow to the heliocentric worldview.
If the swirling flows always behave more like water draining down the inside of a bowl rather than swirling around an outward‐arched surface, that might hint the official geometry is “inverted.”

In short, if direct storm data (e.g., from satellites, drones, or thousands of on‐site sensors) uncovered a repeated, unexplainable pattern of funnel intensification that only the concave model (with outward gravity) could elegantly account for—that would tear a hole in the standard model.

6. Summation of the Devil’s‐Advocate Position

Bowl vs. Dome:

Standard Earth is essentially a dome overhead if you flatten a local region. A hurricane swirling within that dome might be missing a “downward” or “inward” shape to funnel easily.
A concave Earth is more like a bowl or dish, letting fluid swirl to a center “drain” point more naturally.

Curvature Magnitude:

Over 500 km, a 5 km difference in height is nearly half the troposphere’s thickness, not negligible. This might be enough to produce measurable differences in storm structure or intensification.

Gravity Orientation:

If “gravity” is truly an outward push from a central ether, then swirling flows might concentrate more readily near the “lowest point on the inside shell,” matching the eye of a hurricane more naturally than a convex scheme.

Empirical Gap:

If real storms show patterns that deviate from standard (convex) geostrophic or gradient‐wind balances in ways only a “concave geometry + outward gravity” easily explains, it would be a potential falsification of the heliocentric model.

Final Devil’s‐Advocate Verdict

While mainstream meteorology robustly explains hurricanes without needing an inside‐out Earth, one could argue that the “concave sphere” geometry provides a more intuitive funnel mechanism—just like water spinning down a drain.

If, in real data, we find systematic “bowl‐like” features that defy the best spherical‐Earth fluid models, that might reveal a hole in heliocentrism.
In that scenario, the concave Earth theory could claim victory, showing it natively provides the correct funnel shape and intensification, whereas the globe model is forced to jump through hoops.

Of course, actual meteorologists would dispute that such data or anomalies exist. But as a thought experiment, yes—there is a conceivable path for how the “toilet‐bowl–style” concavity argument might defeat the standard model if certain measurements strongly favored a concave geometry.