A Documentational Comprehensive Writeup
Below is a comprehensive writeup documenting and discussing all the main themes and arguments presented in the video regarding a concave Earth model that incorporates a cardioid light path. The video covers how this model reinterprets Eratosthenes’ experiment, proposes local Sun and Moon distances, explains eclipses and parallax, and ultimately claims superiority over the standard (convex) globe model in terms of geometry, balance, and energy efficiency.
The reader should be aware that this version of the explaining of the sun is unique to the model of the Model by YouTuber “Yo No” Sebastián
https://www.youtube.com/@yono1921 -
In the Presented View
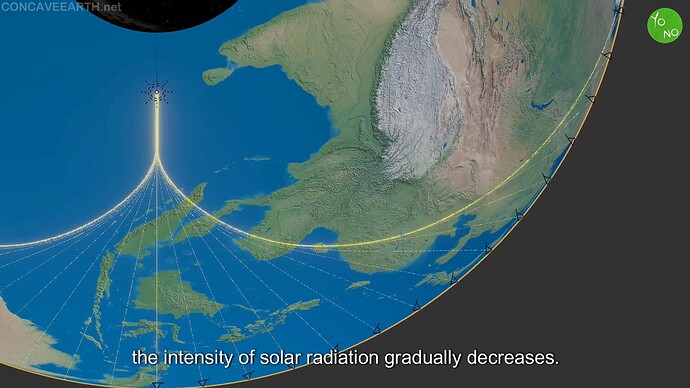
This inside‐out worldview is anchored in the cardioid—a curved shape commonly observed in nature (e.g., diffraction patterns, wave propagation, shells). According to the video, once you assume we live on the inner surface of a spherical shell, with sunlight bending or reflecting in a cardioid‐like path, it becomes possible to replicate many well‐known phenomena conventionally ascribed to a convex Earth.
Eratosthenes’ Experiment: Inside Instead of Outside
A centerpiece of the official model is Eratosthenes’ measurement, which yields a ~40,000 km circumference for Earth. Multiple modern re‐measurements confirm that figure. The flat Earth idea is therefore ruled out. However, this experiment alone does not, in the video’s argument, prove we live on the outside of the sphere.
By employing a “cardioid caustic” inside a concavity, the video shows how sunlight can arrive at the exact same angles Eratosthenes found, except we are standing on a concave inner surface. The video calls this a more “natural” explanation of those angles and contends that we remain on a spherical surface of ~40,000 km circumference, only in reverse.
The Cardioid Trajectory and Multiple Phenomena
Circular Celestial Discs
The video asserts that, in standard perspective, one might expect subtle distortions in the Sun or Moon’s outline if vantage points were changing significantly. Yet we observe consistently circular shapes. Under the concave model, the smooth, uninterrupted bend of the cardioid path ensures those discs appear perfectly round from various locations.
Conservation of Angular Sizes
In mainstream thinking, an object’s angular size typically shifts with distance. The concave/cardioid model proposes a balancing act: as the light path’s curvature changes, the “aperture” also changes proportionally, keeping the Sun’s (or Moon’s) angular diameter near constant. This allegedly explains why the Sun and Moon maintain similar apparent sizes despite moving across the sky.
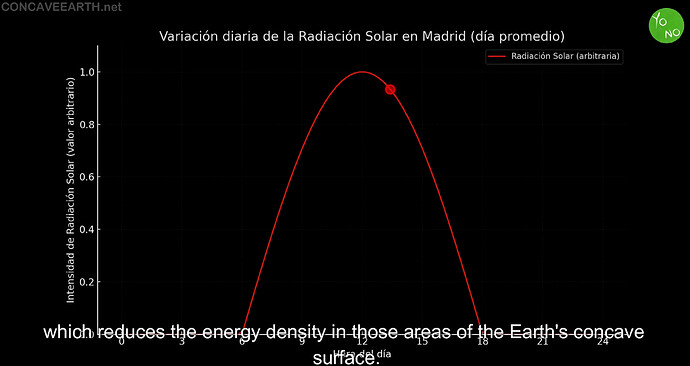
Parabolic Solar Radiation
Observationally, solar intensity peaks around midday. The model credits this to a cardioid‐guided focusing of rays near the local zenith, yielding higher light‐ray density—and thus higher radiation—at noon. Away from zenith, rays curve more or diverge, reducing intensity.
Deriving the Sun and Moon’s Dimensions
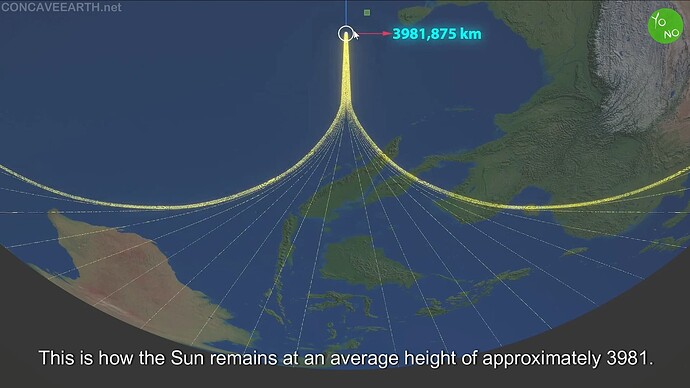
By analyzing how cardioid caustics behave inside a spherical concavity, the video calculates specific altitudes and diameters for the Moon and Sun:
- Moon: ~3,185 km above sea level, with a diameter of ~28.4 km.
- Sun: ~3,982 km high, ~36.9 km in diameter.
These figures are drastically smaller than mainstream science. Yet the video claims they match official parallax data: when observing the Sun and Moon from locations separated by 45° or 90°, the measured separation angles (1.3° or 1.8°) align with the distances derived from this concave geometry.
They further argue that the typical ~270 km diameter of the umbra during a solar eclipse likewise fits neatly with these local, smaller bodies. Rather than a massive Sun far outside Earth’s orbit, the Sun is local—shining from ~4,000 km overhead.
Eclipse Explanations and Lunar Phases
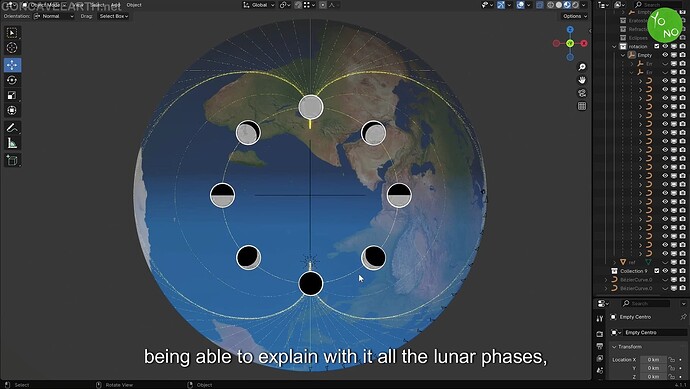
Lunar Eclipse Without Earth’s Shadow
Rotating the cardioid path 180° from the “center of the universe” produces a return of sunlight at the antipode, which the video says accounts for the lunar eclipse—no need for Earth’s external shadow as in the standard model.
Continuity of Lunar Phases
By intercalating the remaining light region, the video completes a full sunlight trajectory, claiming this geometry predicts each lunar phase precisely and matches observed shadows.
Efficiency, Proportion, and Critiques of the Official Model
Sun–Moon Scale Discrepancy
The standard model states the Sun is about 400 times the Moon’s diameter and ~99.99999995% of its radiation goes off into space. This is depicted as inefficient and disproportionate. In the concave model, the Sun is only ~29.9% larger than the Moon (36.9 km vs. 28.4 km in diameter), and nearly 100% of its radiation is used inside the shell, fostering life with minimal waste.
Physical Laws and Energy Conservation
Because so little sunlight is “wasted” in the concave scenario, the video contends it better respects the law of conservation of energy, blackbody radiation, and the second law of thermodynamics. The official model, by contrast, is labeled as “unbalanced,” with vast scales that do not reflect typical natural phenomena, which often rely on simpler, more direct proportions.
Concluding Claims
The cardioid, says the video, is a “fundamental key” that integrates:
- Eratosthenes’ angles (40,000 km sphere size).
- Geometric consistency with solar and lunar parallax.
- Umbra size in eclipses.
- Circular discs of celestial bodies.
- Preserved angular diameters.
- Efficient energy usage and fewer “exaggerated” scales.
Because a flat Earth fails to replicate these phenomena, and the mainstream globe is viewed as wasteful in energy usage with an extreme Sun–Earth size ratio, the video concludes that concavity—shaped by the cardioid path of light—“most likely” represents the true Earth geometry. Eratosthenes, in this reading, does not prove an external sphere but instead reinforces the idea of a concave spheroid.
Hence, the final position is that this inside‐out Earth model, built around cardioid reflection/refraction, surpasses the official model in matters of balance, proportion, and efficiency while cleanly explaining everyday observations, lunar phases, and eclipse shadows—thereby providing a more “perfect” cosmic design.