The Supreme Harmony of the Universe: The Endospherical Field Theory by Paolo Emilio Amico-Roxas 1990

[ConcaveEarth.net]

The Supreme Harmony of the Universe: The Endospherical Field Theory by Paolo Emilio Amico-Roxas

Download the Book

The Supreme Harmony of the Universe The Endospherical Field Theory by Paolo Emilio Amico-Roxas 1990.pdf (7.5 MB)

Overview

The Supreme Harmony of the Universe: The Endospherical Field Theory is a groundbreaking exploration into a novel cosmological model. Written by Paolo Emilio Amico-Roxas, the book introduces the concept of an endospherical universe where Earth is envisioned as a hollow sphere, and humanity resides on the inner surface of this sphere. Within this framework, celestial bodies, energy, and light exist and move inside the sphere rather than in the infinite expanse of traditional space.

This work synthesizes insights from geometry, electromagnetic theory, and ancient philosophical traditions to offer a radically different explanation of the cosmos. Originally published in 1990, it challenges the foundations of conventional science and seeks to unify physics, metaphysics, and cosmology in an elegant new model.

---

Structure and Content

1. Preface

The preface sets the tone for the book by challenging readers to step outside the boundaries of mainstream cosmology. Roxas introduces the idea of geometric inversion, where the relationships between concave and convex geometries become the key to understanding the universe. He traces inspiration from ancient mythologies and cosmological models, emphasizing the need for a paradigm shift in our understanding of the cosmos.

2. Endospherical Field Theory

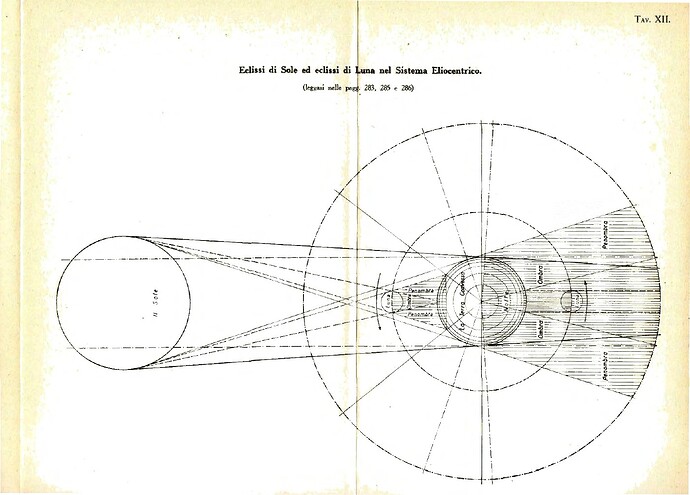
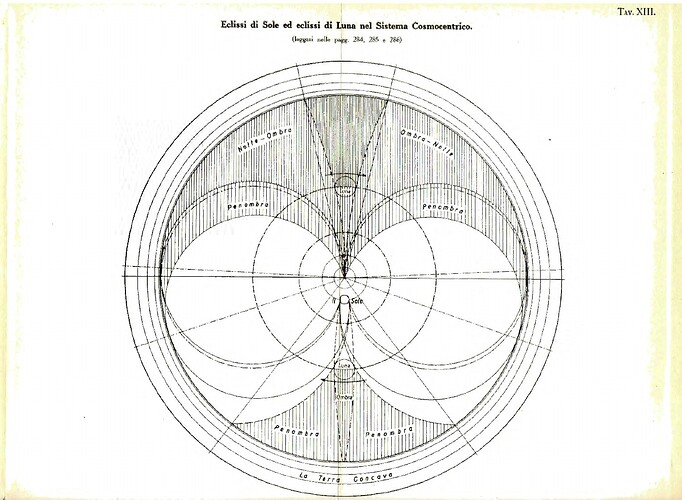
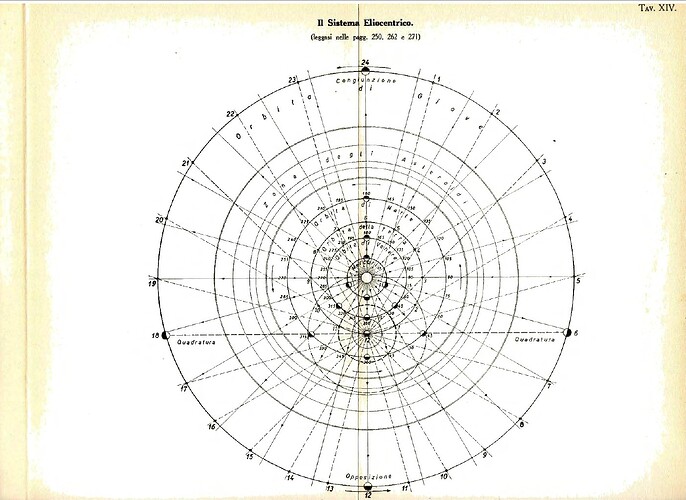
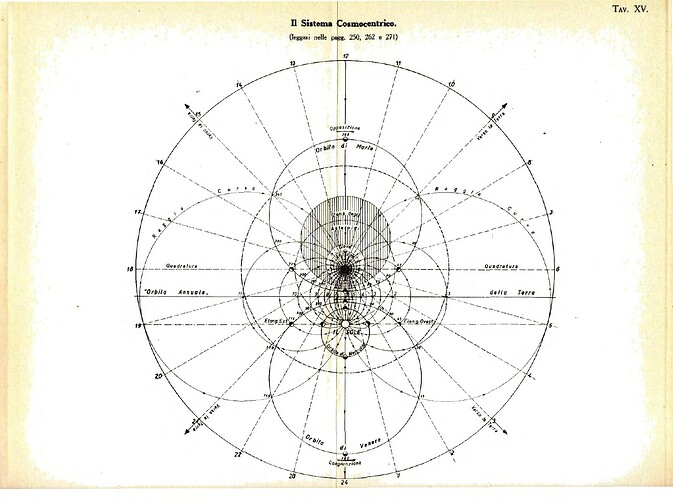
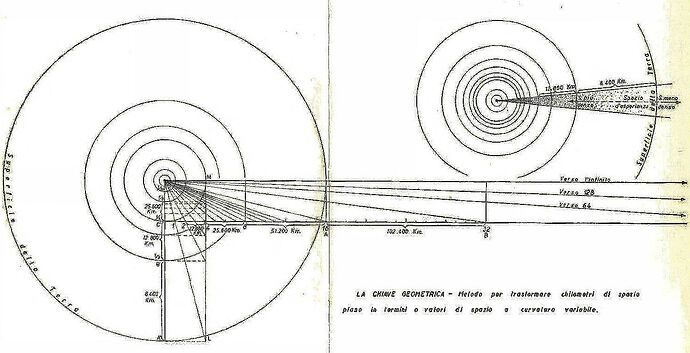
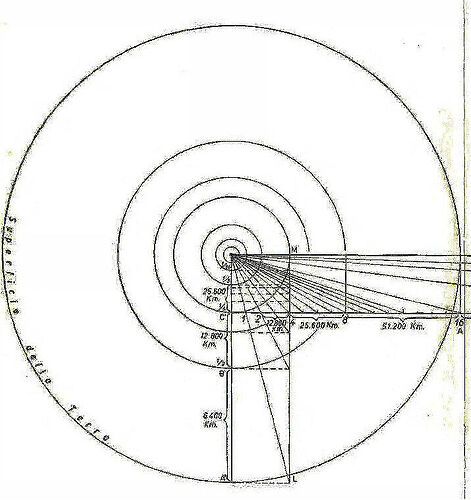
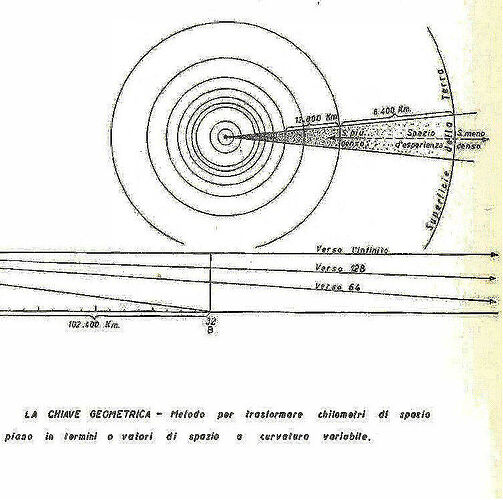
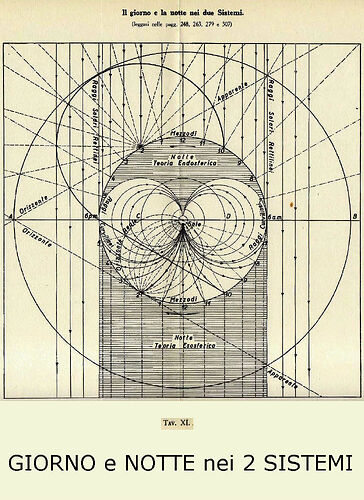
At the core of the book lies the concept of the endospherical field. Roxas proposes that all phenomena within the universe—from light to gravity—are governed by a unified field dynamic. The Earth’s interior shell acts as a boundary, while the universe’s energy flows within this enclosed space. Key points include:

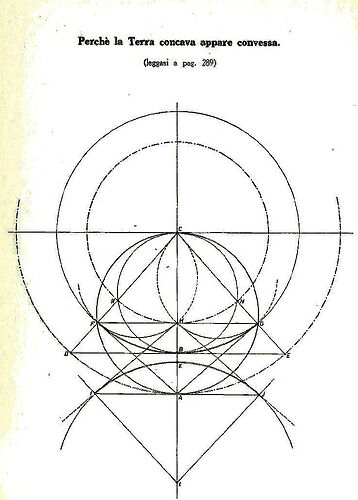
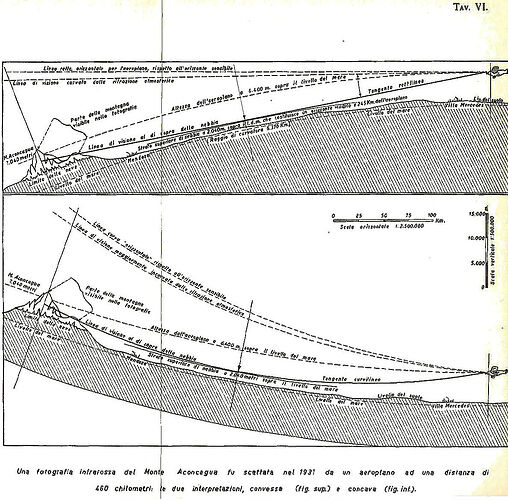
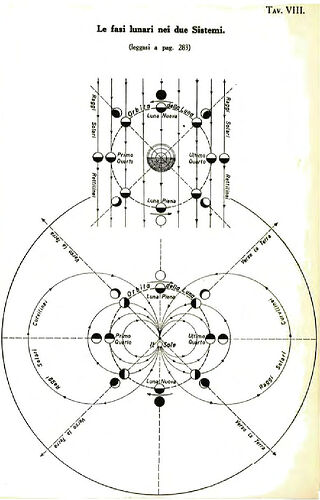
• The redefinition of light as bending upward, creating optical illusions of convexity.
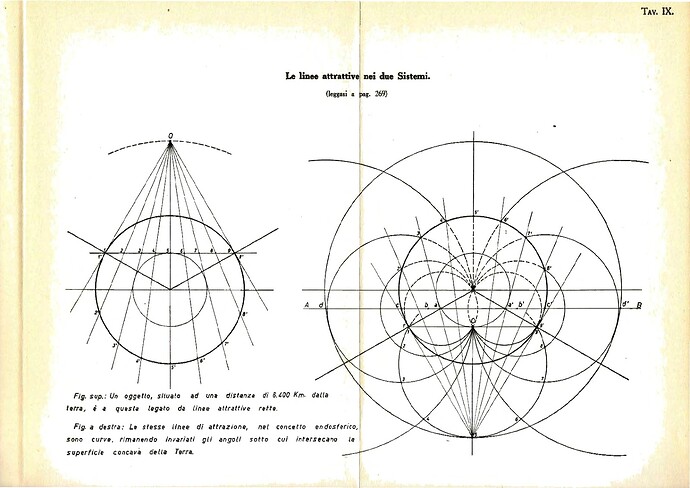
• Gravity as a result of longitudinal pressures rather than mass-based attraction.
• The celestial sphere as the central organizing structure within the endospherical model.

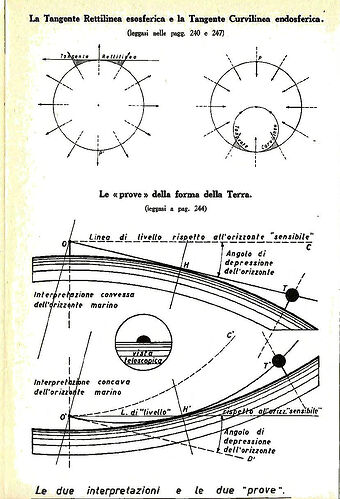
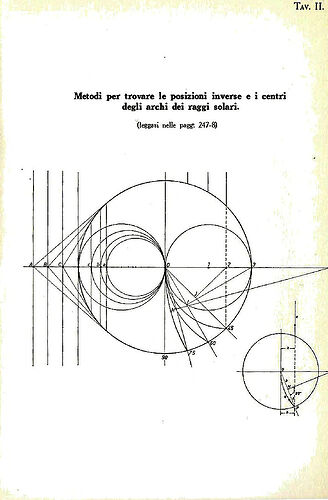
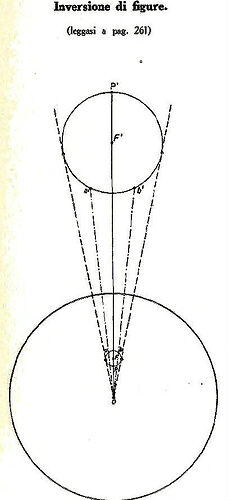
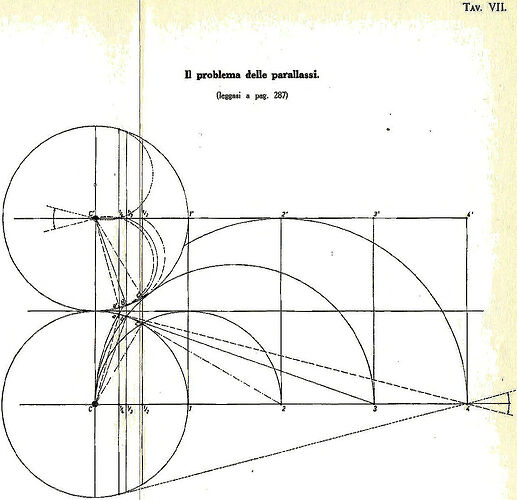
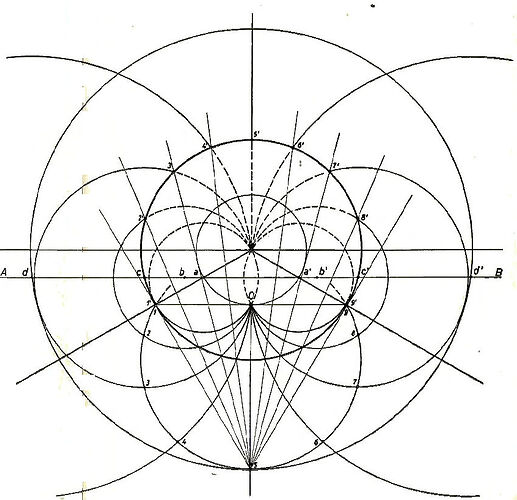
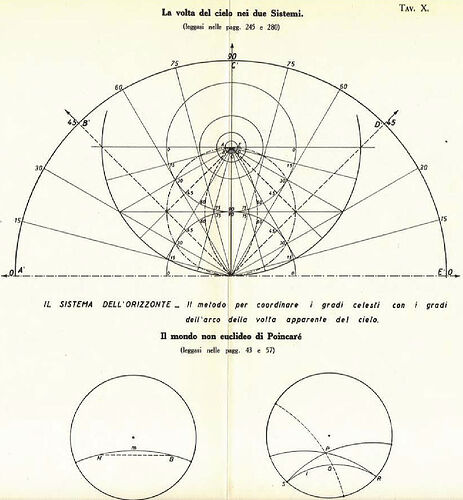
3. Geometric Inversion and the Nature of Light

Roxas provides an extensive discussion on geometric inversion. Using principles of reciprocal radii, he explains how convex geometries can be mathematically transformed into concave structures. He argues that this framework aligns better with observed phenomena such as:

• The curvature of light paths.
• The illusion of an infinite sky.
• The behavior of distant stars and celestial objects.

4. Energy Conservation in a Closed System

One of the significant claims in the book is that the endospherical model resolves inconsistencies in the conservation of energy. Roxas suggests that energy within the sphere is self-contained, circulating in a closed loop from the celestial sphere back to the Sun and stars. This eliminates the paradoxes associated with energy dissipation in infinite space.

5. A Critique of Conventional Cosmology

Roxas critiques the assumptions underpinning mainstream science, including:

• The concept of a light-year and its reliance on linear Euclidean geometry.
• The interpretation of gravity as a force acting over infinite distances.
• The limitations of space-time curvature models in explaining universal phenomena.

6. Philosophical and Metaphysical Dimensions

In this section, Roxas explores the philosophical implications of the endospherical model. Drawing on Neoplatonic and ancient cosmological ideas, he argues for a unified, living cosmos. He contrasts this with the existential void of conventional cosmology, emphasizing harmony, purpose, and the interconnectedness of all things.

---

Key Themes and Insights

• Geometric Transformation: The book’s mathematical foundation lies in the inversion of convex and concave geometries, offering a new way to conceptualize space and motion.
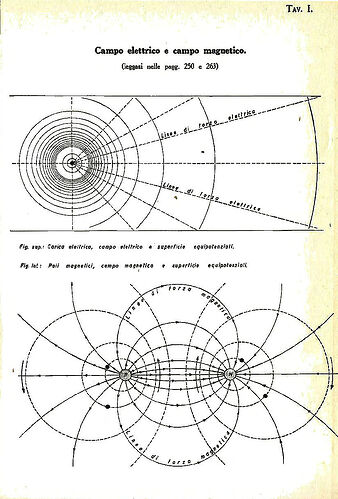
• Unified Field Theory: Roxas correlates electromagnetic phenomena with the behavior of light and gravity in an endospherical model.
• Energy Circulation: The closed-loop energy system within the sphere addresses long-standing questions about energy conservation.
• Optical Illusions: The bending of light upward is presented as the mechanism behind many perceived cosmological phenomena.
• Ancient Wisdom: The alignment of endospherical ideas with ancient cosmologies underscores their timeless relevance.

---

Chapter Summaries

Chapter 1: Geometric Foundations

This chapter introduces geometric inversion, explaining how concave and convex structures relate mathematically. Roxas argues that this principle is crucial for understanding the endospherical model, as it redefines the spatial relationships we observe and aligns them with ancient and modern observations of celestial motion.

Chapter 2: Light and Optics

The behavior of light is reexamined, focusing on its refraction and bending within a concave geometry. Roxas shows how upward-bending light creates the illusion of a convex horizon and distant stars, challenging conventional explanations of optical phenomena.

Chapter 3: Gravity and Field Dynamics

Gravity is redefined as a longitudinal pressure system acting within the endospherical structure. Roxas integrates this concept into a broader field theory, showing how it aligns with observed physical forces while addressing gaps in traditional gravitational models.

Chapter 4: Energy and the Cosmos

Energy conservation is explored within the closed spherical system of the endospherical model. Roxas describes how energy flows cyclically, eliminating the paradoxes of energy loss in infinite space and offering a self-contained cosmological framework.

Chapter 5: Revisiting Ancient Cosmologies

Roxas draws parallels between the endospherical model and ancient cosmological systems, such as Egyptian, Neoplatonic, and Vedic traditions. He argues that these systems intuitively grasped the principles of a living, interconnected universe.

Chapter 6: Philosophical Implications

The final chapter reflects on the spiritual and metaphysical dimensions of the endospherical model. Roxas emphasizes harmony and interconnectedness, proposing that this framework restores purpose and coherence to our understanding of the universe.

---

Conclusion

The Supreme Harmony of the Universe challenges readers to rethink everything they know about the cosmos. By uniting physics, geometry, and philosophy, Roxas provides a compelling alternative to conventional models, encouraging exploration and open-minded inquiry. This book is a must-read for anyone seeking to understand the universe from a radically different perspective.

Images from the book

Paolo Emilio Amico-Roxas Endospherical Field Theory Diagrams Translated
http://joedubs.com/wp-content/uploads/2024/09/Paolo-Emilio-Amico-Roxas-Endospherical-Field-Theory-Diagrams-Translated.pdf

[ConcaveEarth.net]

Chapter I

Transformation by Reciprocal Radii

Transformation by reciprocal radii refers in general to three-dimensional space. I expose this transformation in reference to the plane, or rather to two overlapping planes.

Each point on one of the two planes corresponds to another point on the other plane, and vice versa. Overlapping points are defined as fixed, that is, they correspond to themselves. Fixed are the points of the circumference with respect to which the transformation is carried out.

An important exception is the following: all the points at infinity (i.e., the directions of the infinite number of straight lines) correspond to only one point, the center of the circle with respect to which the transformation is carried out, and vice versa.

The geometric inversion (by reciprocal radii) is a quadratic or Cremona transformation and has the following properties:

• With respect to a circle, it transforms arcs into arcs.
• Transforms straight lines into circles passing through the center of inversion (O).
• The straight line passing through O transforms into itself.

The inversion is an isogonal or conformal correspondence, which means it preserves the angles but reverses their orientation.

The inversion extends to the 3rd coordinate (sphere) with the same properties:

• Spheres are transformed into spheres.
• Planes into spheres passing through the center of inversion, and vice versa.

To the plane at infinity, that is to all directions of space, corresponds the center O′ of the sphere with respect to which the inversion is carried out. We will treat the transformation referred to the plane, for simplicity and clarity. Each internal point of the circle of inversion corresponds to an external one, and vice versa.

In Table I, we considered two circles (however considered overlapping):

• If we overlap the two circles, we will have, in the same figure, the internal curved tangent and the external straight tangent, which correspond to each other.
• The two overlapping points of contact constitute a single fixed point.

At the left in Table II, we have the geometric procedure of inversion, to obtain the internal point of the circle that corresponds to an external point and vice versa.

Given a circle with a radius (e.g., 1 meter), we consider point 2 (2m away from the center of the circle) and draw from 2 the two tangents to the circle, passing through the two contact points a and b. Now we consider the point where the line segment joining a and b intersects the line segment joining 2 with the center of the circle: the point of intersection is 1/2 (half a meter), which is the multiplicative inverse (or reciprocal) of 2 (hence the name inversion or reciprocal radii).

To the generic external point m will correspond the internal point 1/m and vice versa. If it is a point at infinity, then from it are drawn parallel tangents that touch the circle at the endpoints of a diameter of the given circle. To this generic point at infinity will correspond the center of the circle, that is, as already mentioned, to each point at infinity (direction) corresponds exactly one point, the center of the circle of inversion.

To find the center N of a circular arc OP, an arc that corresponds to an external segment of the straight line C, we consider the small figure at the right in Table II where the external non-dashed line segment of C corresponds to the arc OP passing through O and through the fixed point P.

The searched center N is located at the intersection of the extension of the circle’s diameter with the perpendiculars on the midpoint of the chord OP (see Table II).

To the dashed straight Euclidean segment inside the circle of inversion corresponds the completion of the non-Euclidean arc external to the circle (also see Table XI).

Let’s consider Table IV; to each curve in the upper figure corresponds a straight line in the lower figure. The two figures, as already mentioned, should be thought of as overlapping. The upper figure represents the non-Euclidean space; the lower figure represents the Euclidean space (where Euclid's 5th postulate is valid).

• To the straight tangents ab, bc, cd of the Euclidean space (lower figure) correspond the curved tangents ab, bc, cd of the space with variable curvature (upper figure).
• To the straight Euclidean parallels correspond the curved non-Euclidean parallels.
• The angles intersecting the Euclidean lines and the corresponding non-Euclidean lines are identical.

The reversible formulas for the transformation from the classical exospherical cosmos into the endospherical one are:

x = r² x₁ / (x₁² + y₁²)
y = r² y₁ / (x₁² + y₁²)
        

where x₁ and y₁ are the inverse coordinates of x and y.

---

Projectivity

Projectivity (also known as homography or projective transformation) is a bijective algebraic correspondence between S₁ and S′₁ or a bijective and continuous correspondence that preserves cross-ratios.

Involution is a special case of projectivity between two forms of the first kind, where any two elements always correspond in a double way.

The two elements are said to be conjugated in the involution, which has two fixed or double points in each of which two conjugated elements coincide.

A conic establishes a correspondence, subject to the conic, between the points and lines of a plane: this correspondence is called polarity. An involutive correlation between two overlapping planes is a plane polarity.

If a point P and a plane p have a reciprocal correspondence in the polarity, then they are said to be the pole and polar of each other. If the second point lies on the polar of the first, the first will lie on the polar of the second: the two points are said to be conjugated or reciprocal in polarity. A point is called self-conjugate if it lies on its own polar.

A polarity is represented by equations of the form:

pu = a₁₁x + a₁₂y + a₁₃z
pv = a₂₁x + a₂₂y + a₂₃z
pw = a₃₁x + a₃₂y + a₃₃z
        

The condition for two points P(x, y, z) and Q(x′, y′, z′) to be conjugated is:

vx′ + vy′ + wz′ = 0